Wrap Arrays Over Curved Surfaces with OmniSlice®

How do you take a flat pattern or array and conform it to a curved surface without distorting the pattern? It’s a challenging issue. Applications such as frequency-selective surfaces, array antennas, metasurfaces, and diffractive optics often require repeated patterns to be applied to doubly-curved surfaces without deforming the size, shape, and spacing of the elements in the array. Deformations will weaken or completely erase the electromagnetic properties.

Overcoming Deformations

All other current approaches fail because they involve mapping a flat array to the curved surface by various coordinate transform methods. Mapping a planar array to a doubly-curved surface will always produce strong deformations because some elements will be squished while others will be stretched. It is like trying to push a square peg through a round hole.

The EMLab at the University of Texas at El Paso took a different approach to create these seemingly impossible geometries. Instead of mapping, their algorithm works by recreating the array from scratch in the natural coordinates of the curved surface. Kraetonics LLC is working closely with the EMLab to develop software that will make it easy for any person to wrap any array over any surface using EMLab’s breakthrough algorithm. For now, Kraetonics is performing this as a service until the software is released.

Preservational Spatially-Variant Lattices (PSVL)

This technology is called a preservational spatially-variant lattice (PSVL) because it spatially-varies a periodic structure while preserving the size, shape and spacing of the unit cells, or elements. 1-3 In fact, any geometric attribute of any periodic structure can be varied over position while still producing an array that is smooth and continuous.

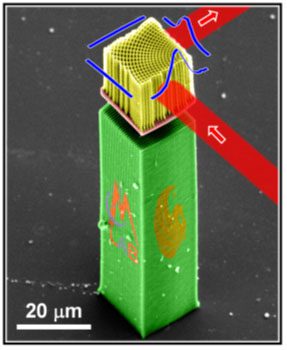
The first-ever functional PSVL was a spatially-variant photonic crystal and was developed by the EMLab at UTEP, in close collaboration with the University of Central Florida, around 2018.  This demonstration achieved a world-record for tightest bend of an unguided optical beam 4. They accomplished this by exploiting the self-collimation effect that would be impossible without the PSVL. This achievement was recognized with Best Photonics Technology by Opli Magazine in 2015. The device is illustrated in the figure below. The blue ribbon in the leftmost diagram indicates the measured transmission through the device.

Spatially-Variant Photonic Crystal for self collimating light beam
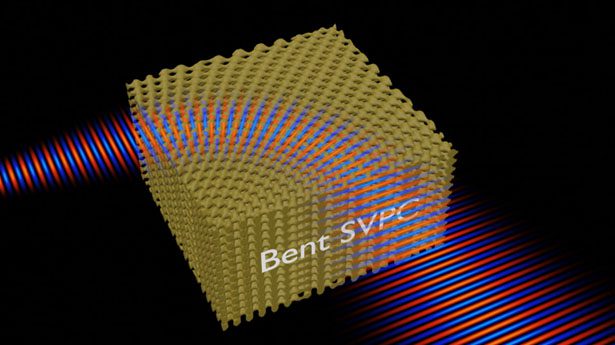
Tightest bend of an unguided optical bean using a spatially-variant photonic crystal

A second PSVL was a frequency selective surface (FSS) wrapped over a doubly-curved surface with very abrupt curvature 5. A FSS is a planar structure that filters radio waves by frequency as they pass through the FSS.

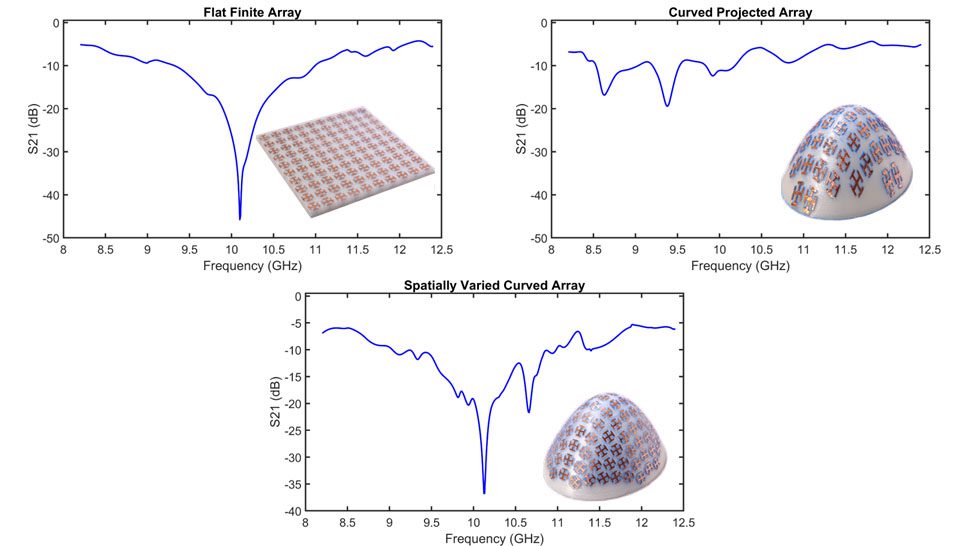
To demonstrate the PSVL algorithm, the EMLab built and tested three devices – a conventional flat FSS, a doubly-curved FSS designed using a conventional projection technique, and a doubly-curved FSS designed using the PSVL algorithm. The PSVL device matched the performance of the flat design, but the second device failed to produce any response at all. These devices and their transmission spectra are shown below.

Transmission spectra of a flat vs doubly curved FSS, and a double-curves FDD designed with the PSVL algorithm

OmniSlice® 3D Printing Software

Kraetonics is building on this breakthrough by developing user-friendly software that will give anyone the ability to wrap arrays over doubly-curved surfaces while preserving the electromagnetic properties of the array. Since these structures will require special manufacturing techniques to produce, Kraetonics has also been developing hybrid 3D printing technology in OmniSlice® specifically for manufacturing conformal arrays.
OmniSlice® gives ordinary three-axis printers the ability to print conformally, even onto near-vertical sidewalls. Using a standard three-axis printer lowers manufacturing costs, improves resolution, and reduces build time compared to six-axis machines that can tilt their printing head.
The figure below shows a FSS printed onto an abrupt and doubly-curved surface using OmniSlice® . The conductive elements were conformally printed onto near-vertical sidewalls using an ordinary three-axis printer without any modifications to the hardware.
FSS printed onto a doubly-curved surface
FSS designed using PSVL in OmniSlice

Interested in learning more about how Kraetonics can help you overcome your design obstacles? Reach out today and lets start a discussion about how we can help. 

References

  1. Martinez, Manuel F., et al. “Formulation of Iterative Finite-Difference Method for Generating Large Spatially Variant Lattices.” Applied Computational Electromagnetics Society Journal 37.2 (2022): 141.
  2. Rumpf, Raymond C., et al. “Spatially variant periodic structures in electromagnetics.” Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 373.2049 (2015): 20140359.
  3.  Rumpf, Raymond C., and Javier Pazos. “Synthesis of spatially variant lattices.” Optics express 20.14 (2012): 15263-15274.
  4. Digaum, Jennefir L., et al. “Tight control of light beams in photonic crystals with spatially-variant lattice orientation.” Optics express 22.21 (2014): 25788-25804.
  5. Valle, Cesar L., Gilbert T. Carranza, and Raymond C. Rumpf. “Conformal frequency selective surfaces for arbitrary curvature.” IEEE Transactions on Antennas and Propagation 71.1 (2022): 612-620.
Scroll to Top